当数明魔法学遇护的零知识证上隐私保
作者:0xAlpha DeriProtocol联合创始人 | 编译:DODO Research团队
zk-SNARK的奇妙世界
想象一下,你能向别人证明自己知道某个秘密,却不用透露秘密本身的内容——这就是zk-SNARK(零知识简洁非交互式知识论证)的魅力所在。作为一个经常和密码学打交道的从业者,我至今仍为这项技术的精妙设计感到惊叹。
让我用一个日常生活中的类比来解释:就好比你向酒店前台证明自己确实预订了房间,但完全不需要出示身份证件或预订确认码。听起来像魔术?这正是数学带给我们的现实魔法。
从问题到证明的四步舞曲
构建zk-SNARK证明就像是在跳一支精心编排的舞蹈,需要经历四个关键步骤:
1. 首先,我们要把问题转化为算术电路——这就像把一道复杂的数学题拆解成基础的加减乘除运算。
2. 接着,将这些运算关系用矩阵公式来表示。
3. 然后,神奇的事情发生了——我们把这些矩阵公式转化为多项式,并找到它们之间的整除关系。
4. 最后,在椭圆曲线的加密空间里完成整个证明过程。
前三步其实都是在做"翻译"工作,把问题用不同的数学语言重新表述。真正精彩的是第四步,利用同态加密技术把证明过程搬到加密空间里进行,就像在镜中世界完成魔术表演,既证明了事实,又保护了秘密。
数学基础:你需要知道这些
理解这篇文章只需要大学一年级的代数知识。唯一可能让人犯怵的是椭圆曲线加密,但其实把它想象成一个具有特殊性质的指数函数就行——关键在于它的逆向计算至今仍是个数学难题。
在正式讲解前,我们先约定一些符号规则:矩阵用粗体大写字母(如A),向量用小写字母加箭头,标量就是普通字母。记住这些,待会看公式就不会晕头转向了。
实战案例:爱丽丝的证明之旅
让我们通过一个具体例子来理解整个过程。假设爱丽丝想证明她知道函数f(x)=x³+x²+5的一个解。虽然这个例子很简单,但它能清晰展示zk-SNARK的核心原理。
有趣的是,即便遇到包含if-else的复杂函数,我们也能轻松转化为类似的算术表达式。比如:
f(x,z) = (z-1)(x²+5) + z(x³+x²+5)
这个技巧让我想起编程中的条件表达式,只不过现在我们用纯数学的方式来表达逻辑分支。
第一步:构建算术电路
我们把f(x)分解成最基本的运算步骤:- s1 = x × x- s2 = s1 × x- s3 = s1 + s2- y = s3 + 5
这就像把一道复杂菜肴的烹饪过程拆解成切菜、炒制、调味等基础动作。每个步骤都形成一个"约束条件",总共4个约束构成了我们的算术电路。
第二步:矩阵的魔法
接下来,我们定义一个见证向量s = [1, x, s1, s2, s3, y],然后构造三个矩阵A、B、C。通过矩阵乘法,我们就能用s·A·s·B = s·C来表示所有约束条件。
这个过程最考验耐心的是逐行构建矩阵,确保每个算术门都能正确对应。就像拼乐高积木,必须确保每个零件都卡在正确的位置。
第三步:多项式的艺术
现在,我们要把这些矩阵转化为多项式。这就像是把离散的数据点连成平滑的曲线。使用拉格朗日插值法,我们可以找到满足条件的多项式PA、PB、PC。
最终我们会得到形如P(z) = t(z)h(z)的等式,其中t(z)是预设的多项式,h(z)是商多项式。这个可整除关系是整个证明的关键所在。
第四步:椭圆曲线上的加密之舞
最精彩的部分来了!我们要在椭圆曲线上完成证明。椭圆曲线密码学就像是在一个特殊的数字宇宙里进行运算,这里的基本单位是曲线上的点。
理解椭圆曲线点加法有个形象的比喻:想象在桌布上画一条曲线,用直尺找到两点间的交点,然后像折纸一样把这个点对称翻转到曲线另一侧,这就是"加法"的结果。
我们还需要引入双线性映射这个神奇工具,它允许我们在加密空间中进行乘法运算。这就像是在戴着手套的情况下完成精细的拼图操作。
完整的证明流程
在实际操作中,我们需要先生成公共参考字符串(称为验证钥VK)。有趣的是,无论问题多复杂,VK始终只需要7个椭圆曲线点。这让我想起万能钥匙的概念——同样的锁具可以保护无数个不同的保险箱。
爱丽丝生成证明的过程本质上是进行了一系列椭圆曲线点的线性组合。而验证过程则像在进行三重安全检查:
1. 确认证明中的点确实是参考点的合法组合
2. 验证各项系数的正确性
3. 检查最终的等式是否成立
为什么这很重要?
作为一个见证了区块链技术发展的从业者,我深刻体会到zk-SNARK的革命性意义。它让我们能在不泄露隐私的前提下完成验证,这在金融、医疗、投票等领域都有巨大应用潜力。
回想第一次理解这个机制时的震撼,就像突然看懂了魔术师的秘密手法。数学的深邃之美,往往就藏在这些看似简单的等式背后。
推荐阅读
Vitalik Buterin的《Zk-SNARKs: Under the Hood》
Thomas Chen等人的《零知识证明综述》
Maksym Petkus的《zk-SNARK工作原理权威解释》
零知识证明相关维基百科条目
相关文章
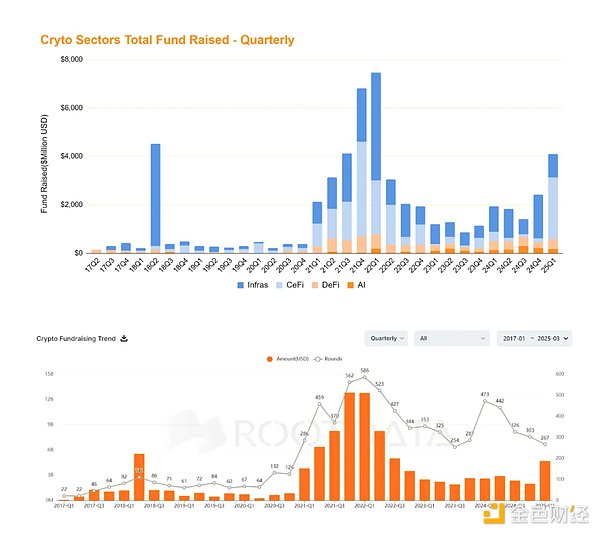 作为一名在加密领域摸爬滚打多年的观察者,最近Arbitrum的表现真是让人捏把汗。记得半年前它刚上线时,整个社区都在期待它能像其他L2项目一样一飞冲天。然而现实却给了所有人一记响亮的耳光 - 进入9月后,ARB居然跌破了0.9美元的心理关口,这简直是在投资者伤口上撒盐。惨淡的市场表现回看这半年,ARB的走势简直可以用"跌跌不休"来形容。我清楚地记得3月20日那天,各大交易所同时上线ARB,0.5美...2025-09-25
作为一名在加密领域摸爬滚打多年的观察者,最近Arbitrum的表现真是让人捏把汗。记得半年前它刚上线时,整个社区都在期待它能像其他L2项目一样一飞冲天。然而现实却给了所有人一记响亮的耳光 - 进入9月后,ARB居然跌破了0.9美元的心理关口,这简直是在投资者伤口上撒盐。惨淡的市场表现回看这半年,ARB的走势简直可以用"跌跌不休"来形容。我清楚地记得3月20日那天,各大交易所同时上线ARB,0.5美...2025-09-25 各位数字资产爱好者们注意啦!我刚发现一个不得了的消息:FBBank的NFT项目正在进行第九期空投活动!说实话,在这个市场行情下还能看到这么慷慨的福利,还真是让人眼前一亮。不容错过的赚钱机会作为一个经常关注区块链空投的老玩家,我得说FBBank这次的玩法确实很吸引人。要知道,现在优质项目的免费空投已经越来越少了,能赶上这一波真的很幸运。我昨天特意研究了一下,发现参与门槛不高,但奖励却相当可观。记得上...2025-09-25
各位数字资产爱好者们注意啦!我刚发现一个不得了的消息:FBBank的NFT项目正在进行第九期空投活动!说实话,在这个市场行情下还能看到这么慷慨的福利,还真是让人眼前一亮。不容错过的赚钱机会作为一个经常关注区块链空投的老玩家,我得说FBBank这次的玩法确实很吸引人。要知道,现在优质项目的免费空投已经越来越少了,能赶上这一波真的很幸运。我昨天特意研究了一下,发现参与门槛不高,但奖励却相当可观。记得上...2025-09-25 还记得30年前那本预言元宇宙的小说《雪崩》吗?它的作者尼尔·史蒂芬森最近可没闲着。这位被尊称为"元宇宙之父"的科幻大师,带着他的创业公司Lamina1和Avalanche区块链平台搞了个大动作——他们要联手打造一个真正开放的元宇宙。说实话,当我第一次听到这个消息时,内心是复杂的。一方面,Meta等科技巨头在元宇宙领域的折戟让人对这个概念产生了怀疑;另一方面,看到原创者亲自下场建设,又让人重新燃起希...2025-09-25
还记得30年前那本预言元宇宙的小说《雪崩》吗?它的作者尼尔·史蒂芬森最近可没闲着。这位被尊称为"元宇宙之父"的科幻大师,带着他的创业公司Lamina1和Avalanche区块链平台搞了个大动作——他们要联手打造一个真正开放的元宇宙。说实话,当我第一次听到这个消息时,内心是复杂的。一方面,Meta等科技巨头在元宇宙领域的折戟让人对这个概念产生了怀疑;另一方面,看到原创者亲自下场建设,又让人重新燃起希...2025-09-25 你知道吗?在加密货币这个大千世界里,有一只"柴犬"正在掀起不小的风浪。没错,我说的就是以那只标志性柴犬头像闻名的狗狗币(Dogecoin)。作为一个曾经见证过2017年加密货币狂热的观察者,我必须说狗狗币的故事特别引人入胜。这只"柴犬"的市场表现记得去年有一次和朋友在咖啡馆闲聊,他突然问我:"你看狗狗币了吗?涨疯了!"我当时的第一反应是:"那个玩笑币?"谁能想到这个最初只是用来调侃加密货币热潮的"...2025-09-25
你知道吗?在加密货币这个大千世界里,有一只"柴犬"正在掀起不小的风浪。没错,我说的就是以那只标志性柴犬头像闻名的狗狗币(Dogecoin)。作为一个曾经见证过2017年加密货币狂热的观察者,我必须说狗狗币的故事特别引人入胜。这只"柴犬"的市场表现记得去年有一次和朋友在咖啡馆闲聊,他突然问我:"你看狗狗币了吗?涨疯了!"我当时的第一反应是:"那个玩笑币?"谁能想到这个最初只是用来调侃加密货币热潮的"...2025-09-25
羊毛党的末日?Hyperliquid用真金白银重新定义加密商业逻辑
说实话,作为一个在加密圈摸爬滚打多年的老韭菜,看到Hyperliquid这波操作我都惊呆了。还记得两年前大家都在Galaxy上刷空投的日子吗?那些靠做任务领糖果的项目现在看起来简直像上个世纪的产物。一场完美的商业逆袭让我们看看Hyperliquid交出的成绩单:市场份额从可怜的0.3%飙升至66%——这个数字让人想起特斯拉当年颠覆传统汽车行业的场景。最让我震惊的是他们的交易量增长曲线:2023年2...2025-09-25 在数字资产市场风云变幻的当下,安全合规问题始终是悬在行业头顶的达摩克利斯之剑。就在最近,区块链安全领域的"守护者"Beosin和托管服务界的"金库管家"Cobo宣布达成战略合作,这消息让不少业内人士都松了口气。安全专家遇上托管巨头说起来,这两家可都是各自领域的"老司机"。Beosin就像区块链世界的"网安卫士",从代码审计到资金追踪,提供的是全生命周期的安全防护。而Cobo更不得了,作为2017年...2025-09-25
在数字资产市场风云变幻的当下,安全合规问题始终是悬在行业头顶的达摩克利斯之剑。就在最近,区块链安全领域的"守护者"Beosin和托管服务界的"金库管家"Cobo宣布达成战略合作,这消息让不少业内人士都松了口气。安全专家遇上托管巨头说起来,这两家可都是各自领域的"老司机"。Beosin就像区块链世界的"网安卫士",从代码审计到资金追踪,提供的是全生命周期的安全防护。而Cobo更不得了,作为2017年...2025-09-25

最新评论